Проблема общих сторон
Конечно, в действительности генерация фрактальных ландшафтов не сводится к примитивному рецепту «изогнуть, разделить, повторить по вкусу». Вам придется проследить за тем, чтобы каждая линия изгибалась только один раз; к тому же ландшафт еще необходимо отобразить на экране, но это уже подробности.
Первая и самая важная деталь заключается в том, что вы должны следить за своими действиями. Если процедура FractureTriangle() будет просто изгибать все грани подряд, у вас получится что-то вроде рис.8.4. Треугольники не будут образовывать сплошную сетчатую поверхность; появятся «плавающие» группы из четырех треугольников, высота вершин которых не будет совпадать с высотой вершин соседей.
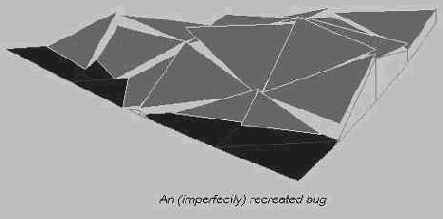
Рис. 8.4. Вот что получается, когда стороны не совпадают
Возможно, рис. 8.5 поможет разобраться в происходящем. Внутренние стороны принадлежат сразу двум треугольникам, мнения которых насчет величины изгиба могут не совпасть. Вершина I является серединой отрезка DF, который принадлежит треугольникам CDF и DEF. Если оба треугольника попытаются самостоятельно задать высоту этой точки, то вершина I в треугольниках 1, 2 и 3 будет находиться на иной высоте, чем она же в треугольниках 4, 5 и 6!
Очевидно, нам потребуется база данных вершин, чтобы положение вершины I можно было задать при обработке треугольника CDF и затем использовать ту же величину смещения для этой вершины при обработке треугольника DEF. Можно попытаться объявить DEF «внутренним» треугольником, рассматривать его в последнюю очередь и использовать «внешние» значения для вершин G, H и I — но взгляните на треугольники GEH и LMN. Отрезки GE и EH принадлежат и «внешним» треугольникам, поэтому для вершин L и M следует использовать «внешние» значения, но отрезок GH находится «полностью внутри», поэтому его необходимо изогнуть. Несомненно, схему с внешними и внутренними треугольниками можно усовершенствовать для правильной обработки таких «внешне-внутренних субтреугольников», но в итоге получится нечитаемый код с высокой вероятностью возникновения ошибок при любых изменениях.
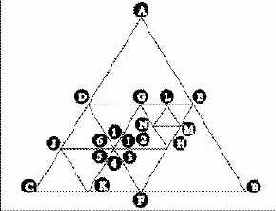
Рис. 8.5. Так треугольники «спорят» из-за вершин
Намного проще определить специальное значение координаты, которое будет присутствовать только у неинициализированных вершин, и заставить FractureTriangle() проверять, не было ли положение середины отрезка задано ранее. Если положение уже задано, FractureTriangle() использует готовое значение; если нет, FractureTriangle() генерирует новую высоту. Возможно, вычисление и просмотр середин внутренних треугольников работают несколько медленнее, чем простая передача аргументов, но программа получается более компактной и наглядной. К тому же на отображение ландшафта неизбеж но уйдет намного больше времени, чем на его расчет.